Code-based cryptography I - Basic concepts and McElice system

Error correction code

在计算机，电信，信息理论和编码理论中，纠错码（ECC，error correction/correcting code）是信息传输中错误检测与纠正的工具。许多系统都会检查数据在传输过程中是否损坏，比如ISBN码的最后一位。
一般来说，通常会讲 $k$ 比特的数据存储为 $n$ 比特，增加 $n-k$ 比特的冗余信息，以便在传输过程中检测和纠正错误。如果没有发生错误，这 $n$ 比特会满足 $n-k$ 个检验方程；否则可以从错误模式中纠正错误。
一个好的纠错码会在引入尽可能少的冗余信息的情况下，纠正尽可能多的错误。
纠错 $t$ 个错误的纠错码并不意味不能纠错 $t+1$ 个错误。

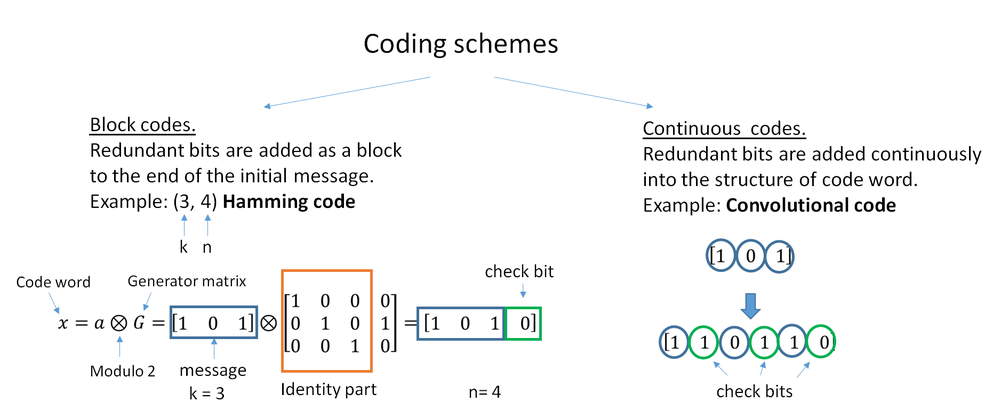
纠错码分为两大类：分组码和卷积码。

  • 分组码适用于一连串固定长度的数据包，而每一种分组码只能用于特定长度的数据包。实际用途中的分组码一般使用硬解码方式，所需时间为每一个数据包长度的多项式时间。
  • 卷积码适用于任意长度的比特流/符号流。接收方通常使用维特比算法将其软解码，但有时也会用其他算法。随着卷积码约束条件的长度增加，维特比解码的解码效率渐近最优；但作为代价，计算时间将以对数式增长。
    error correction code

Linear code

长度为 $n$，维度为 $k$ 的线性码 $C$ 是 $\mathbb{F}_p$ 的 $k$ 维子空间。这样的代码称为q元(q-ary)码。C中的向量称为码字。码的大小是码字的数量，等于$q^k$。
线性码$C$有两种理解方式：

  • 生成矩阵(Geneartor matrix) $G, G\in \mathbb{F}_p^{k*n}$ 的 $k$ 个行向量张成的空间，$C = \{mG | m \in \mathbb{F}_p^k\}$。
  • 校验矩阵(Parity-check matrix) $H$, $C$为由$H$表示的线性变换 $\phi: \mathbb{F}_q^n \rightarrow \mathbb{F}_q^{n-k} $ 的核(kernel space)，$C = \{c \in \mathbb{F}_q^n | cH^T = 0\}$。$H$生成的码称为$C$的对偶码。

线性码的任何线性组合仍然属于该码，因此有线性码的最小距离是最小非零码的汉明重量。

Decoding problem

解码问题(Decoding problem)是指给定$x\in \mathbb{F}_p^n$，找到最接近$x$的码字$c\in C$。令$x=c+e$，$e$是错误向量，注意找到最接近$x$的码字等价于找到最小的汉明重量的错误向量$e$。

  • 如果 $x$ 中存在 $t$ 个错误，即错误向量 $e$ 的汉明重量是 $t$，这被称为 $t-$错误校正问题（t-error correcting problem）。
  • 存在许多具有快速解码算法的编码族，例如里德-所罗门码（Reed-Solomon codes）、戈帕码/交替码（Goppa codes/alternant codes）等。
  • 通常的解码问题是困难的：最好的方法-信息集解码（Information-set decoding）需要指数级时间。

The McEliece cryptosystem

参考Robert McEliece 1978[2]，McEliece密码系统是一种基于编码的公钥密码系统，它的安全性基于解码问题的困难性。
设 $C$ 为长度为 $n$ 的二元 Goppa 码 $\Gamma$，其维数为 $k$，最小距离为 $2t+1$，其中 $t \approx (n-k) / \log_2(n)$；原始参数（1978年）为 $n=1024, k=524, t=50$：

  • McEliece 密钥包含 $\Gamma$ 的生成矩阵 $G$，一个高效的 $\Gamma$ $t$ 错误校正解码算法；一个 $n \times n$ 的置换矩阵 $P$ 和一个非奇异的 $k \times k$ 矩阵 $S$。
  • $n, k, t$ 是公开的；但是 $\Gamma, P, S$ 是随机生成的秘密。
  • McEliece 公钥是 $k \times n$ 矩阵 $G^{\prime} = S G P$。

Encryption

  • 选择一个 $k$ 比特信息向量 $m$，将其编码为 $c = mG^{\prime}$；
  • 产生一个 $n$ 比特，重量为 $t$ 的随机向量 $e$，计算 $y = c + e$；
  • 发送 $y$。

Decryption

  • 接收到 $y$ 后，计算 $yP^{-1} = mG + eP^{-1}$；
  • 由于 $P$ 是置换矩阵，$eP^{-1}$ 仍然是一个重量为 $t$ 的向量；
  • 使用 $\Gamma$ 的 $t$ 错误校正解码算法，找到$mS$ 和 $m$。

Security

攻击者面临的挑战是将 $y$ 解码到由 $G{\prime}$ 生成的码中最近的码字 $mG{\prime}$ 。如果 $G{\prime}$ 不暴露任何特殊结构，这就是一般解码问题。

Reference

[1] https://www.youtube.com/watch?v=9EC2taInna4&list=PL6hzlGxGIS1DcTZq6Fv1yq0_dmqDaNN4v
[2] McEliece R J. A public-key cryptosystem based on algebraic[J]. Coding Thv, 1978, 4244: 114-116.