本篇论文主要介绍了在ZK场景下所使用的Cyclotomic Ring,通过限制素数$p$的选取,从而实现Challenge Set $\mathcal{C}$ 中的元素可逆,从而帮助Ajtai Commitment实现Proof of Knowledge。
首先简要介绍一下Ajtai Commitment
由此可知,如果我们能保证 $\mathcal{C}-\mathcal{C}$ 中的元素可逆,就能保证其Proof of Knowledge的性质
接下来给出结论: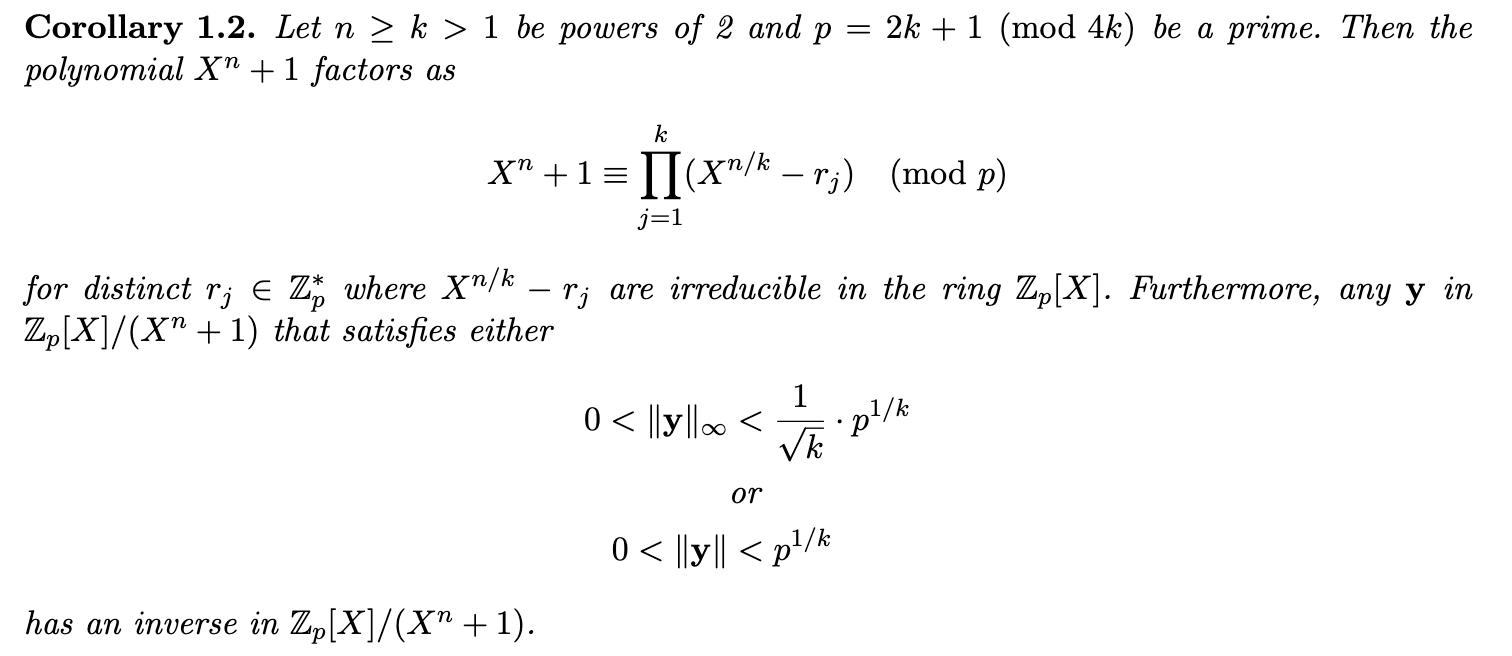
其中 $p=2k+1 \pmod{4k}$的条件是为了保证能够进行分解
之后通过安全参数和Challenge Set的选取,可以获得$\left | y \right |_\infty$ 的值的大小,再通过$k$即可反推出所需要使用的 素数$p$的大小。
其中关于分圆多项式分解等内容的证明还是相对比较有趣,值得一读
其中
- $\Phi_m(X)$是第$m$个循环多项式
- $\delta(m)$是$m$的根式(radical),即$m$的不重复素因子的乘积
将$m$分解为$m = p_1^{e_1} * p_2^{e_2} * \dots * p_r^{e_r}$,
其中 $p_i$ 是不同的素数,那么 $\delta(m) = p_1*p_2*\dots*p_r$ ,是 $m$ 的无平方因子部分。
要证明 $\Phi_m(X) = \Phi_\delta(m)(X^{(m/\delta(m))})$ ,我们可以证明这两个多项式有相同的根。
设$\zeta_m$为本原$m$次单位根。根据循环多项式的定义:
$\Phi_m(X) = ∏_{(j,m)=1} (X - \zeta_m^j)$
其中$(j,m)=1$表示$j$与$m$互素。
我们需要证明的关键是:$X^{(m/\delta(m))} - \zeta_{\delta(m)}^j = 0$的解集合与本原$m$次单位根集合是相同的。
首先证明\alpha是m次单位根
已知$\alpha^{(m/\delta(m))} = \zeta$,且$\zeta$是本原$\delta(m)$次单位根,因此:
$\zeta^{\delta(m)} = 1$
所以: $\alpha^m = \alpha^{(m/\delta(m)·\delta(m))} = \zeta^{\delta(m)} = 1$
这证明了$\alpha$是$m$次单位根。
证明$\alpha$的阶恰好等于m
假设$\alpha$的阶是$d$,即$d$是使得$\alpha^d = 1$的最小正整数。因为$\alpha^m = 1$,所以$d$必须整除$m$(记为$d|m$)。
我们需要证明$d = m$。通过反证法,假设$d < m$。
因为$\alpha^d = 1$,我们可以推导:
$(\alpha^{(m/\delta(m))})^{(d·\delta(m)/m)} = \zeta^{(d·\delta(m)/m)} = 1$
由于$\zeta$是本原$\delta(m)$次单位根,上式表明$\delta(m)$必须整除$(d·\delta(m)/m)$,即:$\delta(m) |(d·\delta(m)/m)$