What Can and Cannot Be Done - Bound in Code

After a long “travel” in coding theory, I finally feel I have understand the Bound. So I come back to write down this blog in case I forget again in the future
In this blog, we will introduce some bounds used in coding theory.

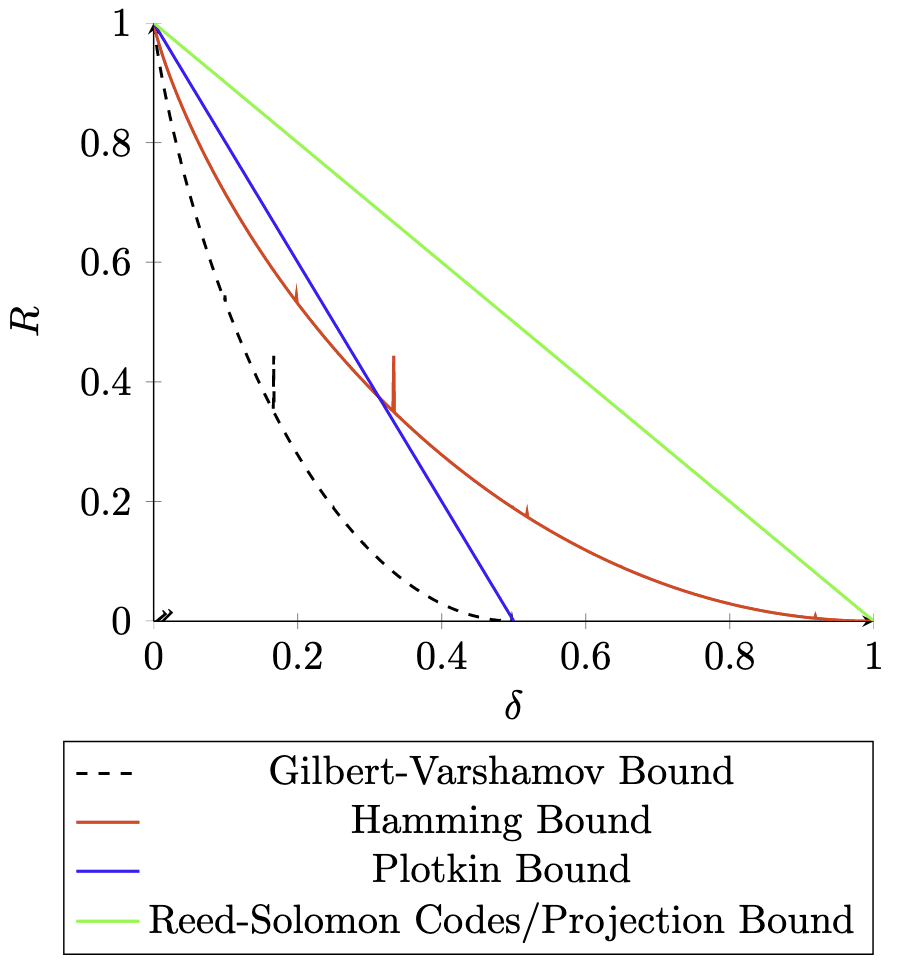
Hamming Bound

Fact 1 Let $C$ be a code with minimum distance $d$. For any $c, c^{\prime} \in C, c \neq c^{\prime}$, we have that $B\left(c,\left\lfloor\frac{d-1}{2}\right\rfloor\right)$ is disjoint from $B\left(c^{\prime},\left\lfloor\frac{d-1}{2}\right\rfloor\right)$.

For Binary Code:

Set $r=\left\lfloor\frac{d-1}{2}\right\rfloor$ ．It follows from Fact 1 that

$$\left|\bigcup_{c \in C} B(c, r)\right|=\sum_{c \in C}|B(c, r)|=|C| \cdot|B(r)|$$

Also

$$\bigcup_{c \in C} B(c, r) \subseteq\{0,1\}^n$$

and so we have

$$\left|\bigcup_{c \in C} B(c, r)\right| \leq 2^n$$

which gives us

$$|C| \leq \frac{2^n}{|B(r)|}$$

Thus，

$$|C| \leq \frac{2^n}{\sum_{i=0}^{\lfloor(d-1) / 2\rfloor}\binom{n}{i}}$$

Similarly, For q-ary case:

$$|C| \leq \frac{q^n}{\sum_{i=0}^{\lfloor(d-1) / 2\rfloor}\binom{n}{i}(q-1)^i}$$

As we all know, the correctable codeword must contain no more than $\lfloor(d-1) / 2\rfloor$ errors. So if we want every codeword to be correctable, the ball must be disjoint

$$\forall \mathcal{C}, |\mathcal{C}| \leq \frac{q^n}{\sum_{i=0}^{\lfloor(d-1) / 2\rfloor}\binom{n}{i}(q-1)^i}$$ $$\forall C \quad R \leq 1-H\left(\frac{\delta}{\Omega}\right)+o(1)$$

Gilbert–Varshamov bound

In my understanding, we can regard GV bound as a greedy approach to construct code.

For Binary Code:

• Set $S=\{0,1\}^n$ and let $C=\emptyset$.
• As long as $S \neq \emptyset$, pick a point $v \in S$ and add $v$ to $C$. Remove $B(v, d-1)$ from $S$, i.e. $S=S \backslash B(v, d-1)$.

Notice that we are removing at most $\sum_{i=0}^{d-1}\binom{n}{i}$ points from $S$ in every iteration. Since we add one element to $C$ in each iteration, we have that

$$|C| \geq \frac{2^n}{\sum_{i=0}^{d-1}\binom{n}{i}}$$

Similarly, For q-ary case:

$$|C| \geq \frac{q^n}{\sum_{i=0}^{d-1}\binom{n}{i}(q-1)^i}$$

This is a constructive proof, so

$$\exists \mathcal{C}, |\mathcal{C}|\geq \frac{q^n}{\sum_{i=0}^{d-1}\binom{n}{i}(q-1)^i}$$ $$\begin{aligned} &\text { When } \delta<\frac{1}{2} \text { : }\\ &\exists C \quad R \geq 1-H(\delta)-o(1) \end{aligned}$$

Plotkin Bound

Plotkin Bound answer the question that

$$\text { What is the best trade-off for } R, \delta \text { ? }$$

The proof proceeds by shortening the codewords. We group the codewords so that they agree on the first $n-n^{\prime}$ places, where $n^{\prime}=\left\lfloor\frac{q d}{q-1}\right\rfloor-1$. In particular, for any $x \in[q]^{n-n^{\prime}}$, define

$$C_x=\left\{\left(c_{n-n^{\prime}+1}, \ldots c_n\right) \mid\left(c_1 \ldots c_N\right) \in C,\left(c_1 \ldots c_{n-n^{\prime}}\right)=x\right\}$$

Define $d=\delta n$. For all $x, C_x$ has distance $d$ as $C$ has distance $d .{ }^1$ Additionally, it has block length $n^{\prime}<\left(\frac{q}{q-1}\right) d$ and thus, $d>\left(1-\frac{1}{q}\right) n^{\prime}$. By sphere-packing bound,

$$|C_x| \leq \frac{q^{n'}}{\sum_{i=0}^{t} \binom{n'}{i}(q-1)^i}$$

this implies that

$$\left|C_x\right| \leq \frac{q d}{q d-(q-1) n^{\prime}} \leq q d$$

where the second inequality follows from the facts that $d>(1-1 / q) n^{\prime}$ and that $q d-(q-1) n^{\prime}$ is an integer.

Note that by the definition of $C_x$ :

$$|C|=\sum_{x \in[q]^{n-n^{\prime}}}\left|C_x\right|$$

which by (1) implies that

$$|C| \leq \sum_{x \in[q]^{n-n^{\prime}}} q d=q^{n-n^{\prime}} \cdot q d \leq q^{n-\frac{q}{q-1} d+o(n)}$$

In other words, $R \leq 1-\left(\frac{q}{q-1}\right) \delta+o(1)$ as desired.

For binary case, we have $R+2\delta \leq 1$

Singleton Bound

$$\text { Let } \mathcal{C} \text { be a code of any alphabet size. Then } \mathcal{C} \text { has rate } R \leq 1-\delta+o(1) \text {. }$$

Delete last $\delta n-1$ coordinates of all codewords in $\mathcal{C}$. All remaining codewords are distinct (as otherwise two identified codewords would have had distance $\delta n-1<\delta n$ ). Further all remaining shortened codewords lie in $\Sigma^{(1-\delta) n+1}$. Therefore $|\mathcal{C}| \leq|\Sigma|^{(1-\delta) n+1}$. So we directly have that the rate is $R \leq 1-\delta+\frac{1}{n}$.

It looks like Singleton Bound above the Plotkin bound. This is possible beacause $R+2\delta \leq 1$ only for binary case